π圆周率是怎么算出来的

π圆周率是我们熟悉的一个概念，在小学时期就已经触及。π约等于3.14是我们背下来的一个参数，那么你知道π值是怎么证明得来的吗，下面我们一起看看π圆周率是怎么算出来，欢迎大家阅读。

π圆周率是怎么算出来的

如果问起π值是怎么来的，也许就有人回答π等于圆周长与直径之比，这只是套公式反推的方法，并不能说明π最初的来源是怎么证明得来的。由于π值是从古至今众多科学家通过各种方法证明而来的，所以π值的来源的算法并没有统一的公式，下面我们以接方面来讲讲π圆周率是怎么算出来的。

1、在中国，圆周率的记载可追溯到古算书《周髀算经》，其上记载 “径一而周三”，意思是直径为1的圆，它的周长为3，即取π=3。显然，该数值还不够精确。此后，数学家先后借助割圆术、无穷级数等方法计算π的值。

2、公元263年，三国时期的数学家刘徽创立了割圆术，用以计算圆周率。他先从圆内接正6边形，逐次分割一直算到圆内接正192边形。他曾说，“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣。”这段话包含了求极限的思想，为我国古代的圆周率计算确立了理论基础。

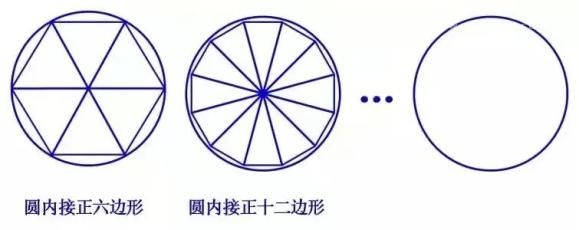
割圆术：用圆内接正多边形的面积去无限逼近圆面积并以此求取圆周率。

刘徽在得出圆周率=3.14之后，发现数值还是偏小，于是继续割圆到1536边形，求出3072边形的面积，终于得到令自己满意的π值3.1416。

3、公元480年左右，南北朝时期的数学家祖冲之不满足于前人的成就，决定攀登新的高峰。他通过割圆术长期刻苦钻研，在儿子祖暅的协助下，反复测算，终于求得了精确度更高的圆周率。《隋书•律历志》中记载了他的成就：

“宋末，南徐州从事史祖冲之更开密法，以圆径一亿为一丈，圆周盈数3丈1尺4寸1分5厘9毫2秒7忽(3.1415927丈)，朒数3丈1尺4寸1分5厘9毫2秒6忽(3.1515926丈)，正数在盈肭之间。密率：圆径113，圆周355。约率：圆径7，周23。”

4、另一个四大文明古国——印度，约在公元530年，数学大师阿耶波多利用384边形的周长，算出圆周率约为√9.8684。 婆罗门笈多采用另一套方法，推论出圆周率等于10的算术平方根。

5、而现代计算机，则常用高斯-勒让德法计算圆周率。计算圆周率公式如下图：

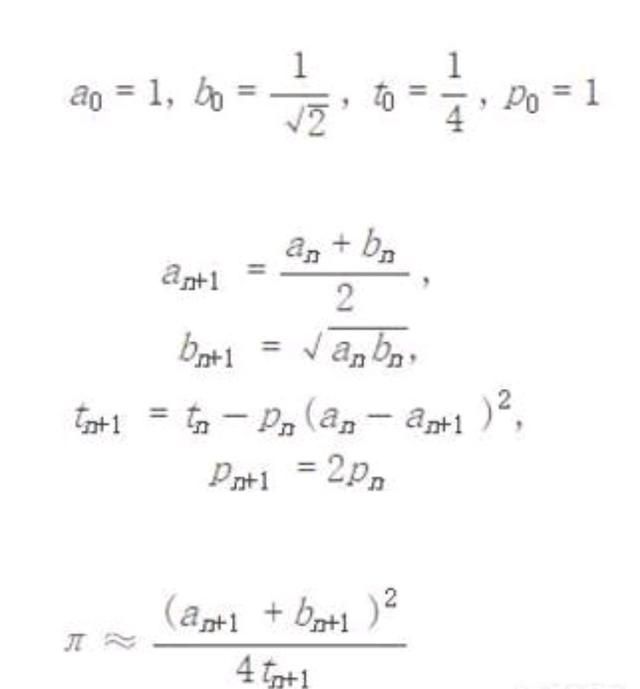
在计算机没有出现之前，数学家们靠手算，经过努力将它算到了528位，这是计算机没有出现之前人类的最高纪录。随着人类科技的快速发展，计算机横空出世，它的到来让数字计算迈上了新台阶，1949年时，可以算至小数点后2037位。到了1973年可以算到100万位，1987算至1亿位，到了2002年1万亿位。到了2011年，已经超过了10万亿位。2019年，谷歌计算到小数点后31.4万亿位。近日 又IBM宣称计算到小数点后60万亿位。几十年来，计算机不断更新升级，圆周率计算创造的一个又一记录，而这个记录一直被打破。

总结：对于π圆周率的来源算法，每个科学家有不同的方法，当下随着社会的进步人们使用计算机可以计算出π值小数点后面几万亿位数，其实使用意义并不大了，只是一种探索的精神，在日常生活中我们普通人只要知道π值等于3.14就已足够。